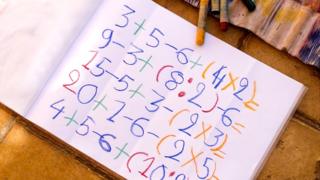Vamos a jugar:
Escoge un número de 4 dígitos en el que al menos 2 sean distintos
Organízalo en orden ascendente y luego en orden descendente
Al número mayor, réstale el menor
Repite
Eventualmente, siempre llegarás al número 6174, algo que se conoce como la constante de Kaprekar. Y si luego repites el proceso, seguirás llegando al número 6174 una y otra vez.
A ver, tratemos con: 4321 – 1234 = 3087; entonces 8730 – 0378 = 8352; y ahora 8532 – 2358 = 6174.
¡Funciona! Después dice que si organizamos 6174 en orden ascendente y descendente para restarlo…
7641 – 1467 = 6174.
Interesante.
Pero probablemente en lo que menos pensaste mientras hacíamos todo esto fue en los símbolos – o =.
Sin embargo, junto con el +, también son interesantes y tienen su historia.
Además, el + está cumpliendo 600 años yel =, 460 años.
= nació del tedio
El símbolo que utilizamos para indicar que estamos por revelar un resultado fue creado por un galés del siglo XVI que a los 14 años ya estaba estudiando en la Universidad de Oxford y a los 21 años enseñaba matemáticas ahí mientras estudiaba medicina.
A los 48 años murió en la cárcel.
Este genio con final trágico se llamaba Robert Recorde y, entre una cosa y otra, escribió varios libros de texto en los que explicó astronomía, geometría y aritmética en inglés, en vez de en latín, como era la costumbre de la época que implicaba que sólo la gente educada podía leerlos.
Escribía para personas comunes y corrientes, y en su último libro, “The Whetstone of Witte” (La piedra de afilar de Witte), publicado en 1557, le dio al mundo el símbolo para “igual”.
Recorde fue un genio pero no entendió una de las reglas más simples de la época en la que vivía.
Recorde dejó la medicina en algún momento de su vida para trabajar en las Casas de Moneda de Bristol, Londres y Dublín como supervisor.
Algo que le molestaba era tener que escribir una y otra vez que un lado de una ecuación era igual al otro lado de ella.
“Para evitar la tediosa repetición de las palabras ‘es igual a’, usaré lo que a menudo uso en mi trabajo: un par de paralelas”, escribió.
¿La razón? “No hay otras dos cosas que puedan ser más iguales”.
Explicación del símbolo = en el libro “The Whetstone of Witte”, publicado hace 460 años.
Se olvidó de las reglas
Además de =, Recorde usó los símbolos alemanes + y -, permitiéndole a la gente expresar ecuaciones matemáticas rápidamente, sin gastar tanta tinta.
No obstante, el latín siguió dominando durante el siglo XVI, de manera que tomó un tiempo antes de que el símbolo = reemplazara a la palabra “aequalis”.
Eventualmente, echó raíces y hoy en día, estés en Siberia o en la Patagonia, puedes escribir esas dos paralelas y te entenderán.
Pero, ¿por qué alguien que además de darnos ese símbolo hizo muchas otras contribuciones de las cuales la ciencia y la informática se siguen beneficiando terminó en la cárcel?
Porque, por genio que fuera, no entendió una de las reglas básicas de su época: la aristocracia siempre gana.
Recorde perdió su trabajo en la Casa de la Moneda de Dublín por decisión del conde de Pembroke. Recorde decidió demandarlo por conducta indebida. El conde le respondió con una demanda por libelo.
El conde ganó.
Recorde desafió al conde de Pembroke. Adivina quién ganó.
✝ ✠ + y el sencillo pero misterioso –
Sumémosle ahora a esta historia el símbolo + y el -, que tampoco son tan antiguos como uno podría imaginarse.
Quizás la manera más simpática de señalar qué hay que hacer en una ecuación para llegar al resultado aparece el papiro de Ahmes, un texto didáctico que contiene varios ejercicios matemáticos:
Un par de piernas caminando hacia adelante indican una suma; caminando hacia atrás indican una resta.
El papiro de Ahmes también es conocido como el papiro matemático Rhind mide 6 metros de largo y 32 centímetros de largo. Es del siglo XVI a. C., pero es una copia de un documento del siglo XIX a. C.
Los griegos, por su parte, los griegos esporádicamente usaban el símbolo / al sumar, pero más que todo expresaban la adición por medio de la yuxtaposición.
Hacia el final del siglo XV, el matemático francés Nicolas Chuquet y el italiano Luca Pacioli usaban “p” (plus) para sumas y “m” (minus) para restas.
Sin embargo, a mediados del siglo XIV el astrónomo Nicole d’Oresme ya había usado el símbolo + como abreviación de “et”, que significa “y” en latín.
De hecho, pocos dudan que el origen de + fue la palabra “et”.
Pero no todos usaban al principio el + que conocemos.
Matemáticos como el escocés David Hume, el neerlandés Christiaan Huygens y el francés Pierre de Fermat usaban la cruz latina “✝”, a veces hasta acostada; el español Juan de Hortega, el inglés Edmond Halley, entre otros, preferían la más ornamental “✠”.
El origen del -, en contraste, no es claro.
Lo que se sabe es que aparece en un manuscrito alemán de 1481 que fue encontrado en la Biblioteca de Dresde. Y en un manuscrito en latín del mismo período aparecen tanto el + como el -. Ambos fueron examinados por Johannes Widmann, que los usa como si fueran conocidos.
Además, su “Aritmética Mercantil” publicada en 1489 fue el primer libro impreso en el que aparecen los dos símbolos que aún usamos para indicar sumas y restas.